Contact: bowen-at-waseda.jp (replace -at- with @)
Research
Thin-film theory
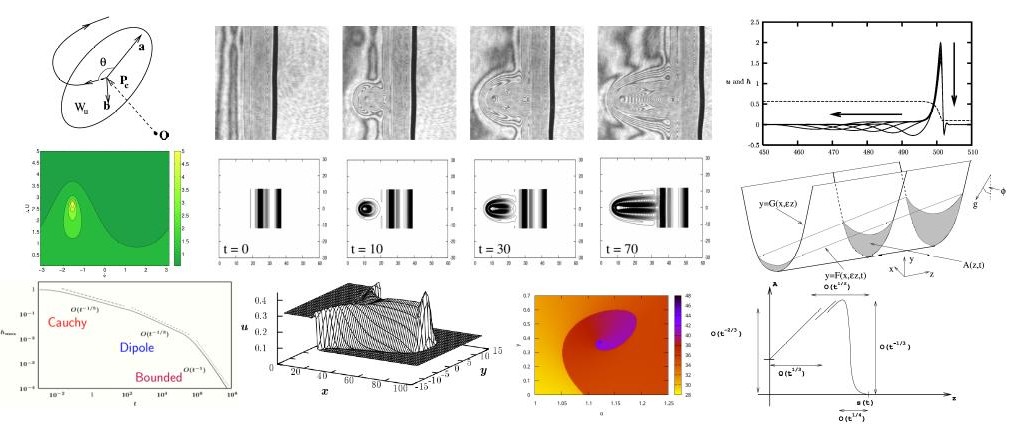
Thin liquid films arise in applications throughout nature, the natural sciences, engineering and industry. The mathematical modelling of such phenomena often yields evolution equations for the interfacial film thickness in the form of (high-order) degenerate parabolic equations.
Analysis of free-boundary problems based on these equations considering, for example, rupture phenomena, moving contact lines and the effects of surface topography and driving forces upon the motion of the liquid requires a combination of analytical methods (e.g. perturbation theory, bifurcation theory, dynamical systems, self-similarity) and numerical techniques (e.g. shooting methods, boundary value solvers, ADI computations) in order to make progress.
The results of this research are also fundamental in understanding the behaviour of other degenerate parabolic partial differential equations. The mathematical methodologies are also applicable to a wide range of problems beyond the scope of thin film theory.
Research group members
Current members
- 2025-2026: Yaxin Luo (UG)
- 2025-2026: Sameer Sharma (UG)
Previous members
- 2024-2025: Matthew Widjaja (UG)
- 2024-2025: Katerina Allegracia (UG)
- 2023-2024: Gylbert Andry (UG)
- 2019: Allen Wong (UG)
Publications
- Touchdown-singularity formation and criticality in the thin-film equation, J. R. King and M. Bowen, Phil. Trans. Roy. Soc. A, 383, 20230375, 2025.
- Cauchy-Dirichlet Problems for the Porous Medium Equation, M. Bowen, J. R. King and T. P. Witelski, Disc. Cont. Dyn. Sys., 43(3&4): 1143-1174. doi: 10.3934/dcds.2022182, 2023.
- Pressure-dipole solutions of the thin-film equation, M. Bowen and T. P. Witelski, Euro. J. Appl. Math., 30 (2), 358-399, 2019.
- On self-similar thermal rupture of thin liquid sheets, M. Bowen and B. S. Tilley Phys. Flu., 25 (10), 102105, 2013.
- Dynamics of a viscous thread on a non-planar substrate, M. Bowen and J. R. King, J. Eng. Math., 80 (1), 39-62, 2013.
- Thermally induced van der Waals rupture of thin viscous fluid sheets, M. Bowen and B. S. Tilley, Phys. Flu., 24 (3), 032106, 2012.
- The linear limit of the dipole problem for the thin film equation, M. Bowen and T. P. Witelski, SIAM J. Appl. Math., 66 (5), 1727-1748, 2006.
- Thermocapillary control of rupture in thin viscous fluid sheets, B. S. Tilley and M. Bowen, J. Flu. Mech., 541, 399, 2005.
- Nonlinear dynamics of two-dimensional undercompressive shocks, M. Bowen, J. Sur, A. L. Bertozzi, R. P. Behringer, Physica D, 209 (1-4), 36-48, 2005.
- The self-similar solution for draining in the thin film equation, J. B. Van Den Berg, M. Bowen, J. R. King, M. M. A. El-Sheikh, Euro. J. Appl. Math., 15 (3), 329, 2004.
- ADI schemes for higher-order nonlinear diffusion equations, T. P. Witelski and M. Bowen, Appl. Num. Math., 45 (2-3), 331-351, 2003
- Thin film dynamics: theory and applications, A. L. Bertozzi and M. Bowen, Modern Methods in Scientific Computing and Applications, 31-79, 2002.
- Intermediate asymptotics of the porous medium equation with sign changes, J. Hulshof, J. R. King, M. Bowen, Adv Diff. Eq., 6 (9), 1115-1152, 2001.
- Anomalous exponents and dipole solutions for the thin film equation, J. Hulshof, J. R. King, M. Bowen., SIAM J. Appl. Math., 62 (1), 149-179, 2001.
- Moving boundary problems and non-uniqueness for the thin film equation, J. R. King and M. Bowen, Euro. J. Appl. Math., 12, 321356, 2001.
- Asymptotic behaviour of the thin film equation in bounded domains, M. Bowen and J. R. King, Euro. J. Appl. Math., 12 (2), 135-157, 2001.
Interdisciplinary articles
- The Language of Mathematics: A Corpus-based Analysis of Research Article Writing in a Neglected Field, L. Anthony and M. Bowen, Asian ESP J., 9(2), 5-25, 2013.
Online material
- Singular perturbation theory, T. P. Witelski and M. Bowen, Scholarpedia 4 (4), 3951, 2009.
Books

Errata for the textbook can be found here. Please email me with any errata/typos that you find.
Educational activities
Major in Mathematical Sciences
I am currently Chair of the Major in Mathematical Sciences here at Waseda University. We offer a four year Bachelor’s course in mathematics taught in English.
Teaching
I currently teach classes in calculus, real analysis and differential equations.
I have previously taught classes in single and multivariable variable calculus, linear algebra, ordinary and partial differential equations, nonlinear dynamics, computational methods, asymptotics and perturbation methods, and fluid mechanics.

President’s Award
I was awarded the President’s Award for Teaching (Spring Semester 2015) by President Kamata of Waseda University.
An example lecture
In the calculus courses, we start from first principles, proving all of the important results as we progress towards increasingly more advanced concepts.
Back in 2019, I gave a “non-technical” introductory lecture to prospective students (and families) visiting Waseda University for an open day, as an example of the kind of material that would be presented at the very beginning of an introductory calculus course. This lecture can be found on YouTube as Mathematics in Action.
Society Membership
- American Physical Society (APS)
- Society for Industrial and Applied Mathematics (SIAM)
- Japanese Society for Industrial and Applied Mathematics (JSIAM)
- Mathematical Society of Japan
- Japan Society of Fluid Mechanics
- American Mathematical Society (AMS)